2の補数表現における数値の表現範囲

解答：ウ

2進数において負の整数を2の補数で表現するときの数値の表現範囲は以下のとおりである。

この式のnにけた数である8をあてはめて表現範囲を求める。

－2^8-1～2^8-1－1
＝－2⁷～2⁷－1
＝－128～127

よって, 解答群のウが正解である。

2進数では10進数のような符号を付けない。

10進数では負の数は－を付けて表現するが、2進数では符号を付けて表現しない。2進数において負の数の表現は、正の数値の2の補数で負の数を表現することが多い。

2の補数は正の2進数表現した数値の各けたすべての1と0を反転させ、1を加えたものである。反転とは1だったら0、0だったら1にすることである。1と0を反転させたものを1の補数という。

2の補数＝1の補数＋1

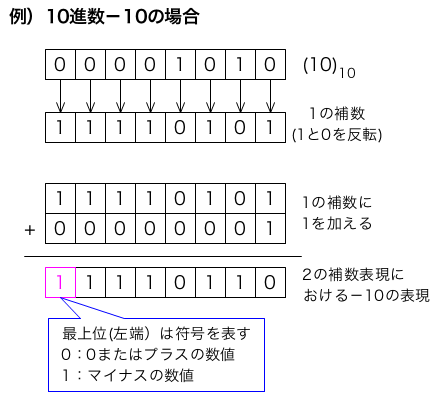
最上位（左端）のけた（ビット）に注目する。

負の数値を2の補数で表現されている数値を10進数に変換する場合、最上位ビットに注目する。最上位ビットが0の場合はそのまま10進数に変換し、1の場合はその2進数は負の数である。その2進数の2の補数を求め、その数値を10進数に変換する。

最上位ビットを意識することを習慣にしてほしい。